3. Algorithmes heuristiques¶
Matière à réfléchir – Tour du monde
Vous avez décidé de faire le tour du monde. Choisissez cinq pays que vous souhaitez visiter et placez‑les sur une carte. Essayez de trouver le meilleur itinéraire pour visiter ces cinq pays.
Quels critères avez‑vous pris en compte pour décider du meilleur itinéraire ? Avez‑vous essayé de trouver la plus petite distance à parcourir ?
Vous avez décidé de visiter dix pays. Est‑ce qu’il est aussi facile de trouver un itinéraire optimal ?
Imaginez que vous souhaitez visiter tous les pays du monde (un peu moins de \(200\)). Combien y a‑t‑il d’itinéraires possibles ? Comment s’appelle ce nombre ?
Si le calcul d’un itinéraire prenait \(1\) milliseconde, combien de temps faudrait‑il pour trouver la meilleure solution en énumérant toutes les solutions possibles ? Pour comparaison, le nombre d’atomes dans l’univers est d’ordre \(10^{80}\).
3.1. Complexité exponentielle¶
Il existe des problèmes difficiles à résoudre. Nous allons nous pencher sur un problème qui s’appelle le problème du sac à dos. Prenons un sac à dos et une multitude d’objets qui ont chacun un poids. Notre objectif est de choisir les objets à mettre dans le sac à dos pour le remplir au maximum, mais sans dépasser sa capacité. Donc la question que l’on se pose est la suivante : quels objets devrions‑nous emporter, sans dépasser le poids maximal que le sac à dos peut contenir ?
Exercice 1 – Le problème du sac à dos
Comment procéderiez‑vous pour résoudre ce problème du sac à dos ? Prenez le temps d’imaginer un algorithme qui puisse résoudre ce problème ?
Appliquer cet algorithme pour \(4\) objets de poids \(1\), \(3\), \(5\) et \(7\) \(kg\) et un sac de capacité de \(10\) \(kg\).
Est‑ce que votre algorithme donne toujours la meilleure solution ?
Solution 1 – Le problème du sac à dos
L’algorithme le plus simple pour résoudre ce problème est un algorithme de force brute (ou un algorithme exhaustif), qui consiste à énumérer toutes les combinaisons d’objets que pourrait contenir le sac à dos, l’une après l’autre, et de calculer le poids total pour chaque combinaison. Après avoir calculé toutes les combinaisons, il suffit de sélectionner la combinaison dont le poids se rapproche le plus de la capacité du sac à dos, sans la dépasser. Vous trouverez ci‑dessous la solution pour l’exemple de l’exercice précédent (« oui » signifie que l’on met l’objet dans le sac à dos et « non » signifie que l’on ne met pas l’objet dans le sac à dos).
+ Combinaison |
\(1 kg\) |
\(3 kg\) |
\(5 kg\) |
\(7 kg\) |
Poids total + |
|---|---|---|---|---|---|
1 |
non |
non |
non |
non |
\(0 kg\) |
2 |
oui |
non |
non |
non |
\(1 kg\) |
3 |
non |
oui |
non |
non |
\(3 kg\) |
4 |
oui |
oui |
non |
non |
\(4 kg\) |
5 |
non |
non |
oui |
non |
\(5 kg\) |
6 |
oui |
non |
oui |
non |
\(6 kg\) |
7 |
non |
oui |
oui |
non |
\(8 kg\) |
8 |
oui |
oui |
oui |
non |
\(9 kg\) |
9 |
non |
non |
non |
oui |
\(7 kg\) |
10 |
oui |
non |
non |
oui |
\(8 kg\) |
11 |
non |
oui |
non |
oui |
\(10 kg\) |
12 |
oui |
oui |
non |
oui |
\(11 kg\) |
13 |
non |
non |
oui |
oui |
\(12 kg\) |
14 |
oui |
non |
oui |
oui |
\(13 kg\) |
15 |
non |
oui |
oui |
oui |
\(15 kg\) |
16 |
oui |
oui |
oui |
oui |
\(16 kg\) |
La meilleure solution se trouve à la 11ème ligne, la capacité du sac à dos (\(10\) \(kg\)) est atteinte lorsqu’on y met le deuxième et le quatrième objet.
Exercice 2 – Le problème du sac à dos avec 10 objets
Combien de combinaisons possibles existent pour le problème du sac à dos avec 10 objets ?
Solution 2 – Le problème du sac à dos avec 10 objets
Mais, combien y a‑t‑il de combinaisons possibles si on a \(10\) objets ? Pour chaque objet, on a deux choix possibles : le mettre dans le sac à dos ou ne pas le mettre dans le sac à dos (to take or not to take, that is the question). Comme ces deux possibilités existent pour chacun des \(10\) objets, le nombre de combinaisons possibles vaut :
\(2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 2^{10}\)
Pour \(n\) objets, le nombre de solutions possibles est \(2^{n}\). Si on a \(2\) objets, il y a donc \(4\) combinaisons différentes d’objets dans le sac à dos (aucun objet, le premier objet, le deuxième objet et les deux objets ensemble). Pour \(3\) objets, le nombre de combinaisons est \(8\). Pour \(5\) objets, nous avons \(32\) possibilités à explorer. Mais déjà pour \(10\) objets, ce nombre dépasse les \(1000\) combinaisons possibles. Pour \(100\) objets, ce nombre devient prohibitif et vaut \(10^{30}\). Si on doit résoudre ce problème avec \(270\) objets sous la main, le nombre de combinaisons possibles dépasse le nombre d’atomes dans l’univers, c’est‑à‑dire \(10^{80}\). Si le calcul du poids d’une combinaison prenait une microseconde, il nous faudrait pour résoudre ce problème bien plus que le temps de l’existence de l’univers, plus de \(14\) milliards d’années. Ces nombres sont réellement vertigineux. Cela va de soi, nous n’avons pas tout ce temps à disposition…
L’ordre de complexité de type \(2^{n}\) est un ordre de complexité exponentielle. Cela vaut aussi pour d’autres constantes que \(2\), par exemple \(10^{n}\) ou \(1.1^{n}\). Lorsqu’un algorithme est d’ordre de complexité exponentielle, cela veut dire que le temps nécessaire pour résoudre le problème croît exponentiellement en fonction de la taille des données \(n\) (voir figure ci‑dessous). Les problèmes de complexité exponentielle ne peuvent être résolus dans un temps raisonnable, pour des données à partir d’une certaine taille.
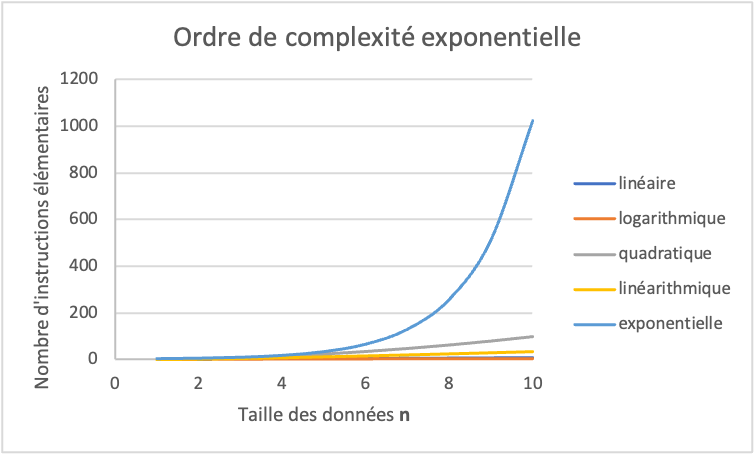
Fig. 3.1 Complexité exponentielle. Comparaison de l’ordre de complexité exponentielle avec les ordres de complexité vus jusqu’ici. Dans un ordre de complexité exponentielle, le nombre d’instructions élémentaires grandit très rapidement avec la taille des données, et l’algorithme est très lent.¶
Lorsqu’il est trop difficile de trouver une solution exacte à un problème, nous ne devons pas nous avouer vaincus. Dans ce cas, nous pouvons tout de même rechercher une solution inexacte, mais qui se rapproche autant que possible de la solution optimale. Les algorithmes qui aboutissent à des solutions non optimales ou inexactes, sont appelés des heuristiques.
Un algorithme heuristique pour le problème du sac à dos pourrait être l’algorithme suivant : prendre les objets du plus petit au plus grand poids jusqu’à remplir le sac à dos, ce qui nous permettrait de mettre le plus d’objets possible. En suivant cet algorithme heuristique, dans l’exemple du premier exercice, on prendrait les trois premiers objets et on aurait un sac à dos rempli à \(9 kg\) au lieu des \(10 kg\) de capacité maximale du sac à dos. Cette solution est suffisamment proche de la meilleure solution, mais elle n’est pas la meilleure solution.
Une solution heuristique est donc une solution intuitive, qui se base sur une stratégie d’essais et d’erreurs, qui en quelque sorte repose sur la chance. Un algorithme heuristique est plus rapide que l’algorithme de force brute qui énumérerait toutes les solutions possibles afin de trouver la meilleure solution, mais on paie le prix de cette efficacité par de la précision. Un algorithme heuristique aboutit à une solution moins précise et moins complète, à une solution sans garantie. Quand un problème est trop complexe, il ne peut être résolu que par des algorithmes heuristiques, aboutissant dans certains cas à des mauvaises solutions.
Le saviez-vous ? – Que veut dire heuristique ?
Le mot heuristique nous vient du grec ancien, plus précisément du terme heuriskêin, qui veut dire trouver, inventer, découvrir.
Ce même terme a donné un autre mot bien connu eurêka.
L’algorithme heuristique qu’on vient de voir est en fait un algorithme glouton, un algorithme qui choisit une solution localement optimale (qui choisit la meilleure solution en apparence à un moment donné) sans se préoccuper de toutes les solutions possibles. On espère ainsi que toutes ces décisions localement optimales mènent vers une très bonne solution. C’est un peu comme si on cherchait à atteindre le plus haut sommet d’une montagne, entourés de brouillard, et qu’on prenait une décision sur le chemin à emprunter uniquement en fonction de ce que l’on peut voir juste autour de nous. On pourrait prendre le chemin le plus pentu en espérant qu’il nous mène à un sommet très haut, mais une fois arrivés en haut d’un sommet, on ne peut savoir si notre sommet est bien le plus haut. On l’espère…
Il n’y a pas que des heuristiques gloutonnes. Un autre exemple de solution heuristique, très utilisée dans les jeux vidéos, est le calcul de distance entre deux objets. Ce calcul est très important par exemple lorsque l’on souhaite détecter si deux objets sont en collision. Pythagore nous dit que cette distance vaut la racine carrée de la somme de \(a\) et \(b\) au carré. Mais ce calcul est difficile, et même si on peut le calculer de manière exacte, il prend beaucoup de temps à calculer s’il y a beaucoup d’objets affichés à l’écran. On préfère ainsi estimer cette distance par un calcul bien plus simple \(a+b\), que l’on sait faux, mais qui est suffisamment proche lorsque les objets sont alignés (voir la figure ci‑dessous).
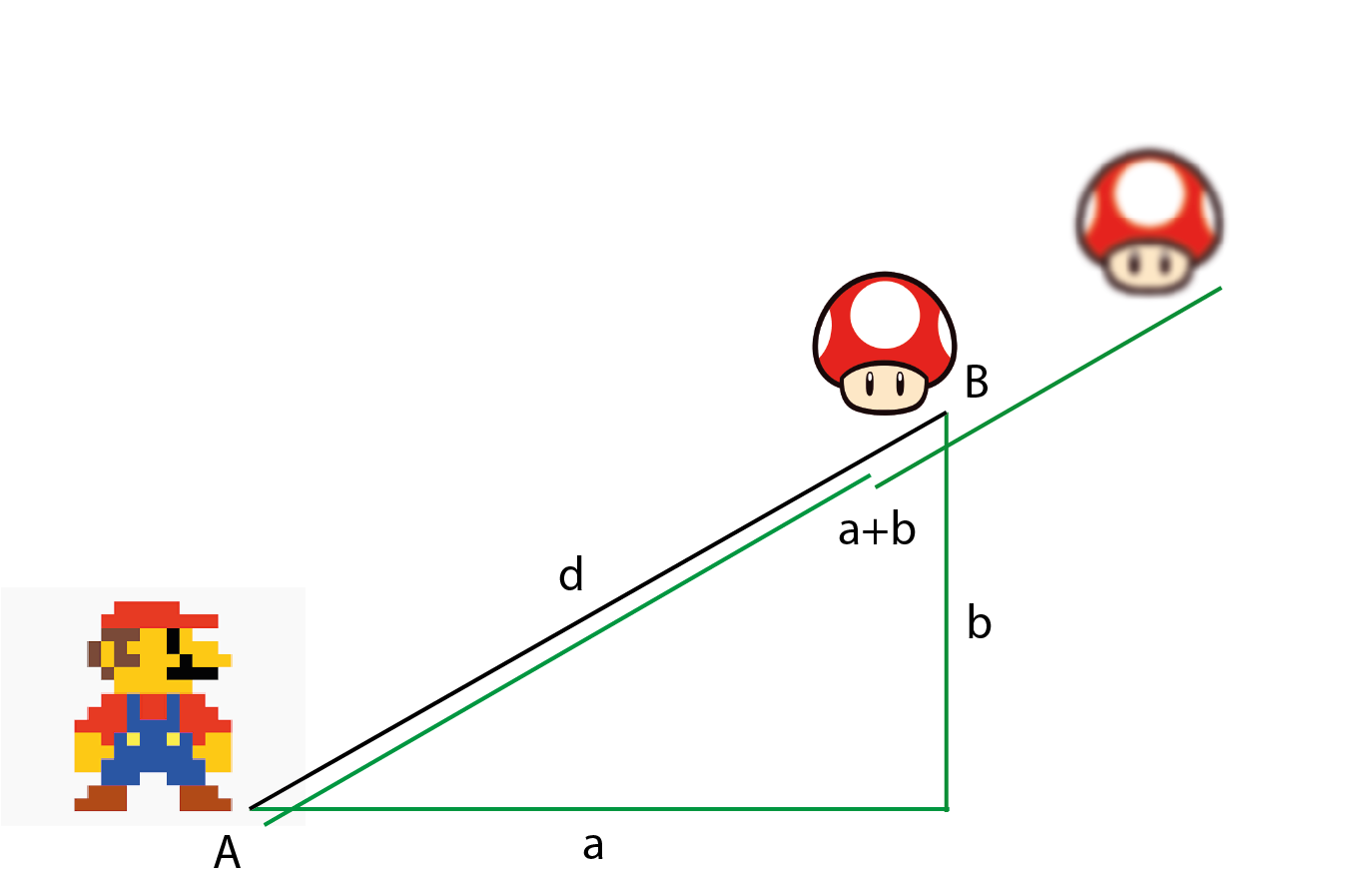
Fig. 3.2 Exemple d’heuristique. Dans les jeux vidéos, on préfère estimer la distance \(d\) entre deux objets \(A\) et \(B\) par la somme des longueurs des côtés de l’angle droit \(a+b\), plutôt que de calculer la racine carrée de la somme des carrés des longueurs des côtés de l’angle droit \(d^{2} = a^{2} + b^{2}\) (théorème de Pythagore). Même si ce calcul est inexact, il est beaucoup plus rapide à calculer quand il y a beaucoup d’objets à afficher à l’écran, et il est suffisamment précis lorsque les deux objets sont alignés.¶
Il existe encore d’autres types d’algorithmes heuristiques, plus lents, mais qui permettent de s’approcher davantage de la solution optimale. Ils utilisent par exemple des stratégies de résolution statistiques, génétiques ou neuronales. L’apprentissage automatique à qui l’on doit les succès récents de l’intelligence artificielle repose sur des algorithmes heuristiques. La majorité des problèmes que l’on tente de résoudre aujourd’hui sont difficiles et leurs algorithmes de résolution ne trouvent pas la meilleure solution.
Pour aller plus loin
Voici un problème à un million de dollars, un parmi les sept problèmes mathématiques du prix du millénaire qui rapporteront de l’argent à la personne qui les résoudra.
On appelle la classe des problèmes qui sont faciles à résoudre la classe des problèmes \(P\). Ces algorithmes peuvent être résolus en un temps polynomial en fonction de la taille des données \(n\), ou \(O(n^{a})\).
Une autre classe de problèmes sont les problèmes difficiles à résoudre qui sont d’ordre de complexité exponentielle. Lorsqu’on arrive à vérifier rapidement (en temps polynomial) si une solution proposée permet de résoudre le problème, il s’agit d’une classe de problèmes appellée \(NP\) ou « non déterministe polynomial ».
On souhaite savoir si les problèmes \(NP\) peuvent être résolus en un temps \(P\) ou non, ou en d’autres termes : est‑ce que \(P = NP\) ?
S’il s’avérait que c’est bien le cas (ce qui est tout de même peu probable), beaucoup de problèmes difficiles à résoudre deviendraient d’un seul coup plus faciles à résoudre. Un des ces problèmes est le problème de repliement des protéines en biologie qui cherche de nouveaux médicaments. Cela pourrait également signifier la fin de la cryptographie telle qu’elle existe actuellement.
3.2. Exercices¶
Exercice 3 – L’univers dans un sac à dos
L’âge estimé de l’univers est de 14 milliards d’années. Si le calcul d’une combinaison d’objets dans le problème du sac à dos prenait une microseconde, pour quel nombre d’objets serait‑il possible de trouver une solution exacte sans dépasser l’âge de l’univers ?
Exercice 4 – Parcours du parcours du parcours de listes
Quelle est la complexité d’un algorithme qui pour chacun des éléments d’une liste de \(n\) éléments, doit parcourir tous les éléments d’une autre liste de \(n\) éléments, puis pour chacune des combinaisons de deux éléments doit encore parcourir une troisième liste de \(n\) éléments ?
Si vous avez besoin de travailler sur un exemple plus concret, quelle est complexité de l’algorithme qui calcule tous les menus possibles d’un restaurant à partir d’une liste de \(n\) entrées, une liste de \(n\) plats et une liste de \(n\) desserts ?
Ai-je compris ?
Vérifiez votre compréhension :
Je sais reconnaître un algorithme de force brute.
Je sais reconnaître un algorithme heuristique.
Je sais reconnaître un algorithme glouton.
Je comprends pourquoi un algorithme de complexité exponentielle est lent.