10. TP Additionneur

Dans cette section, nous allons explorer d’abord la porte ou exclusif (OU-X), qui nous sert à construire un additionneur simple. Nous modifions l’additionneur simple pour en créer un additionneur complet qui prend en compte la retenue. Cet additionneur 1 bit nous sert à construire des circuits pour créer d’autres opérations telles que :

• addition

• soustraction

• incrémentation

• décrémentation

10.1. Clock et fréquence

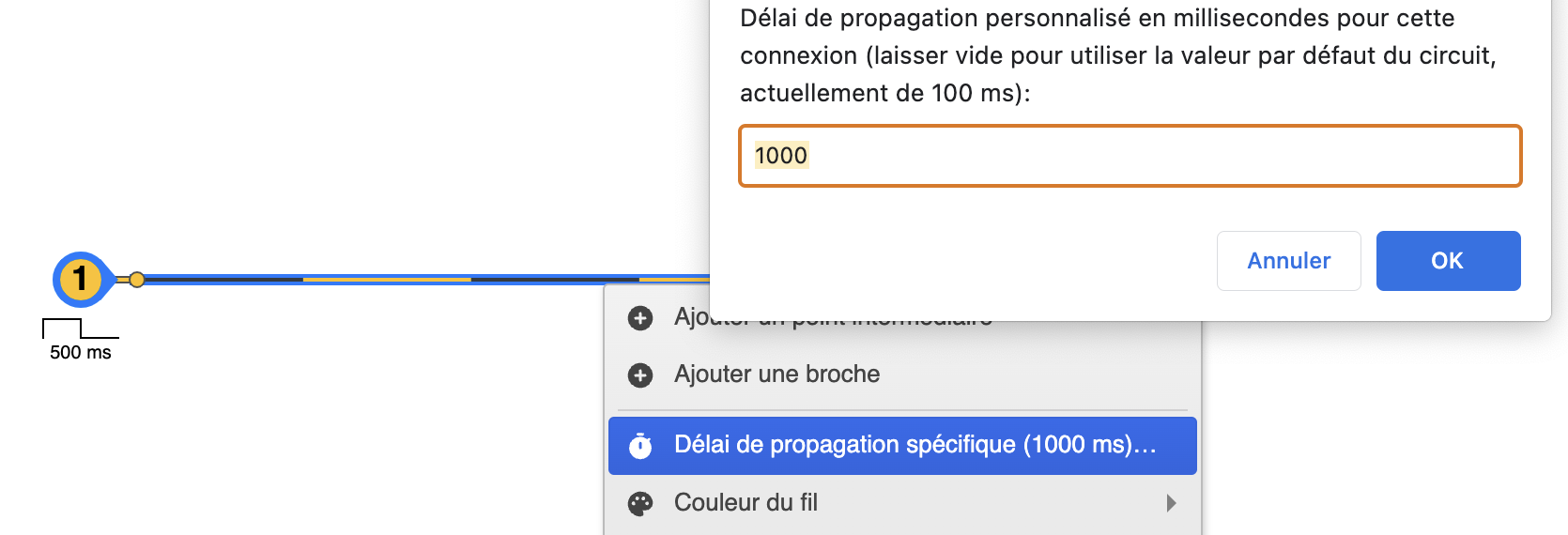
L’entrée horloge (clock) produit un signal qui alterne entre 0 et 1. L’horloge ci-dessous a une période de 500 ms. Le délai de transmission a été mis à 1000 ms. Ceci fait apparaitre 2 cycles du signal (en jaune). On peut donc visualiser la fréquence du signal qui est de 2 Hz.

• Ajoutez une deuxième horloge avec une période de 250 ms.

• Visualisez cette fréquence avec un délai de propagation de 1000 ms.

• Quelle est sa fréquence ? Mettez-la comme étiquette.

• Faites la même chose avec une troisième horloge qui a une période de 100 ms.

Rappel : pour choisir le délai de propagation, cliquez avec le bouton droit sur le fil et sélectionnez le menu contextuel Délai de propagation spécifique…. Mettez-le à 1000.

10.2. Porte OU-X

Une porte OU-X (ou exclusif) avec 2 entrées donne une sortie 1 si exactement une des entrées est 1.

• Montrez la table de vérité pour la porte OU-X.

• Ajoutez 3 portes OU-X et mettez les entrées à 01, 10, et 11

• Créez une porte OU-X avec 3 entrées et observez son comportement

Comment se comporte une porte OU-X avec plus que 2 entrées ?

10.3. Construire un OU-X

Comment peut-on construire un circuit OU-X avec des portes de base (NON, OU, ET) ? Regardons d’abord la table de vérité.

a	b	OU-X
0	0	0
0	1	1
1	0	1
1	1	0

Le circuit ci-dessous représente une porte OU exclusive (OU-X). Mais il y a multiples façons de créer un circuit logique spécifique à partir des éléments de base.

Créez une deuxième façon pour obtenir une porte OU exclusive en partant de l’observation :

(not a and b) or (b and not a)

Utilisez donc :

• 2 portes NON

• 2 portes ET

• 1 porte OU

10.4. Détecteur de parité

Une porte ou exclusif est un détecteur de parité (pair/impair). La sortie d’une porte ou exclusif est 1 si le nombre des entrées actives est impair.

Ajoutez encore 6 portes OU-X et complétez la table de vérité pour les 8 combinaisons possibles:

• pair : 000, 011, 101, 110

• impair : 001, 010, 100, 111

Pour détecter si un nombre d’entrées est pair, il suffit d’ajouter un NON à la sortie du OU-X. On appelle ce circuit un NON-OU-X.

10.5. Multiples commutateurs

La porte OU-X permet d’allumer et éteindre une lampe avec des commutateurs multiples.

Dans le schéma ci-dessous, on peut allumer la lumière dans une pièce à partir de la porte d’entrée et de la cuisine.

Ajoutez un circuit pour qu’on puisse également l’allumer depuis la chambre.

10.6. Addition binaire

Nous avons maintenant tous les éléments pour construire un additionneur binaire. Rappelons-nous que l’addition binaire est très simple.

A	B	A+B	C	S
0	0	0	0	0
0	1	1	0	1
1	0	1	0	1
1	1	2	1	0

Le résultat A+B peut être 0, 1 ou 2. Nous avons besoin de deux bits pour représenter le résultat :

• le bit de somme S

• le bit de retenue C (carry en anglais)

En regardant la table de vérité, on constate que :

• la somme S est exprimée par la fonction OU-X

• la retenue C est exprimée par la fonction ET

Vous trouvez le circuit ci-dessous à droite. Vérifiez sa fonction en cliquant sur ses entrées.

Ajoutez encore 3 demi-additionneurs et montrez la table de vérité pour les 4 conditions d’entrée : 00, 01, 10, 11.

10.7. Additionneur complet

Dans le cas général de l’addition, nous n’additionnons pas deux bits, mais deux nombres à plusieurs bits. Voici l’addition en colonne de deux nombres 4 bits (3+11=14).

 0011
+1011
-----
 1110

Pour être explicite, nous introduisons une ligne supplémentaire qui représente la retenue (C = carry).

 0110 (retenue)
 0011
+1011
-----
 1110

L’additionneur de 2 bits de la section précédente n’est plus suffisant. Pour le cas général, nous avons besoin d’un additionneur qui additionne 3 bits. Il faut tenir compte de la retenue (Cin), qu’il faut inclure dans l’addition. Voici donc la table de vérité pour un additionneur complet.

Cin	A	B	Cin+A+B	Cout	S
0	0	0	0	0	0
0	0	1	1	0	1
0	1	0	1	0	1
0	1	1	2	1	0
1	0	0	1	0	1
1	0	1	2	1	0
1	1	0	2	1	0
1	1	1	3	1	1

Regardez les colonnes et essayez de comprendre avec quelles portes on pourrait le construire. Vous constatez que la colonne S représente la parité. On pourra donc la construire avec des portes OU-X.

• Ajoutez les deux fils qui manquent à l’entrée de la porte ET pour que le circuit produise le signal Cout et se comporte comme un additionneur complet.

• Ajoutez des entrées et sorties au bloc de l’additionneur complet et vérifiez son fonctionnement.

10.8. Additionneur 4 bits

Pour additionner deux nombres 4-bits (quartets) nous avons besoin de 4 additionneurs complets. Chaque sortie Cout est liée à la l’entrée Cin de l’additionneur suivant.

Pour additionner a et b vous devez additionner les bits correspondants: a0+b0, a1+b1, etc.

• Ajoutez les circuits manquants pour additionner deux nombres 4-bits.

• Montrez l’addition de 7+5 dont le résultat devrait être 12.

10.9. Incrémenter (i++)

Additionner 1 à un nombre binaire est une opération très fréquente. Elle est utilisée pour incrémenter le compteur de programme pc (program counter), pour pointer à la prochaine instruction.

Complétez le circuit pour incrémenter la variable i. Dans beaucoup de langages de programmation, une variable incrémentée est désignée par i++.
En Python nous écrivons i = i + 1.

D’ailleurs le nom du langage de programmation C++ est une référence à cet opérateur d’incrémentation.

10.10. Décrémenter (i--)

Soustraire 1 à un nombre binaire est une opération très fréquente. Elle est utilisée pour décrémenter un compteur de boucle i, un pointeur de pile sp (stack pointer), ou un pointeur p vers les adresses de la mémoire.

Complétez le circuit pour décrémenter la variable i. Dans beaucoup de langages de programmation, une variable incrémentée est désignée par i--.
En Python nous écrivons i = i - 1.

Astuce : pour décrémenter la valeur i il suffit d’additionner 1111 qui représente la valeur -1 en format signé.

10.11. Changer de signe (-i)

Les nombres signés sont représentés avec le format complément à deux. Pour un nombre 4-bits, ceci nous donne une plage de -8 à +7 pour des entiers relatifs, et une plage de 0 à 15 pour des entiers naturels. Nous constatons que la plage signée n’est pas symétrique: le côté négatif compte un nombre en plus.

L’opération pour trouver le nombre négatif est: inverser tous les bits (symbolisé par ~) et additionner 1.
Mathématiquement nous pouvons exprimer cette opération comme:

-i = ~i + 1

Par exemple, pour obtenir la représentation binaire de -1 nous inversons 0001, ce qui donne 1110 et nous additionnons 1, ce qui donne 1111.

Complétez le circuit pour inverser le signe de la variable i et obtenir son négatif -i

10.12. Soustraction (a-b)

Pour soustraire deux nombres a-b il suffit d’additionner le nombre négatif du deuxième (-b). Ce nombre négatif peut être obtenu en inversant tous les bits et additionner 1.
Donc -b = ~b + 1.

Complétez le circuit pour soustraire a-b. Le résultat de 10-3 devrait être 7.

10.13. Inversion commutée

L’inverseur commuté permet d’inverser tous les 4 bits d’un nombre avec un signal de contrôle inv :

• pour inv = 0 la sortie est inchangée (a)

• pour inv = 1 la sortie est inversée (~a)

Ajoutez un inverseur commuté pour obtenir ~a ou a selon l’état du sélecteur.

10.14. Négation commutée

Complétez le circuit pour pouvoir obtenir -a ou a selon l’état du sélecteur neg :

• pour neg = 0 la sortie est inchangée (a)

• pour neg = 1 la sortie change de signe (-a)

10.15. Soustraction commutée

Complétez le circuit pour pouvoir obtenir une opération différente selon l’état du sélecteur sub :

• pour sub = 1 les opérandes sont soustraits (a-b)

• pour sub = 0 les opérandes sont additionnés (a+b)

10.16. Les fanions (flags)

Les fanions (flag) sont des signaux qui caractérisent un nombre.

• N pour indiquer que le nombre est négatif

• Z pour indiquer que le nombre est zéro

• P pour indiquer que le nombre de bits à 1 est pair

Par exemple pour le nombre 1001 (-7) on aura N=1, Z=0 et P=1.

Prudence

Faites attention à la différence entre la parité du nombre et la parité des bits.

• la parité du nombre est exprimée par le bit de poids faible (b0),

• la parité du nombre des bits est obtenue avec une opération OU-X (ou exclusif).

Complétez le circuit pour correctement afficher les fanions N, Z et P.