15. Réseauter - points¶
En mathématique un graphe est un ensemble de points liés par des lignes.
De façon générale les points sont des objets, souvent appelés nœuds ou sommets.
Les lignes sont souvent appelées liens ou arêtes.
La Théorie des graphes est une branche des mathématiques. En informatique le graphe est un outil important pour modéliser :
des réseaux sociaux (Facebook)
des réseaux de transportation (Google Maps)
des réseaux informatiques (Internet)
15.1. Les points¶
Nous commençons par une liste de points que nous énumérons à partir de zéro.
15.2. Énumérer¶
Nous pouvons énumérer les points de façon plus compacts en utilisant la fonction enumerate
qui associe un entier à chaque élément d’une séquence.
Le plus souvent enumerate est utilisé dans une boucle ou un veut
parcourir une séquence, mais en même temps on a besoin d’un index i.
Ou dans le cas de notre liste de points
15.3. Les lignes¶
Voici un graphe
15.4. Graphe circulaire¶
Le graphe circulaire parcourt les points une seule fois et forme un parcours circulaire.
Exercice 1
Ajoutez un point supplémentaire, par exemple à (0, -50) ou ailleurs, ainsi que les lignes nécessaires pour garder un graphe circulaire.
15.5. Graphe étoilé¶
Le graphe étoilé est un graphe avec un point spécial, qui est lié à tous les autres points.
Exercice 2
Ajoutez un point supplémentaire, par exemple à (0, -50) ou ailleurs, ainsi que les lignes nécessaires pour garder un graphe étoilé.
15.6. Graphe roue¶
Le graphe roue est le composé d’un graphe circulaire et un graphe étoilé. Un point spécial lie tous les autres points, qui eux sont reliés par un parcours circulaire.
Exercice 3
Ajoutez un point supplémentaire, par exemple à (0, -50) ou ailleurs, ainsi que les lignes nécessaires pour garder un graphe roue.
15.7. Graphe complet¶
Le graphe complet est un graphe ou tous les points sont reliés avec tous les autres points.
Exercice 4
Ajoutez un point supplémentaire, par exemple à (0, -50) ou ailleurs, ainsi que les lignes nécessaires pour garder un graphe complet.
15.8. Attribut des points¶
Les coordonnées ne sont pas nécessaires pour la structure d’un graphe. Dans le sens mathématique, un graphe est uniquement déterminé par ses connexions.
Mais pour dessiner une forme spécifique, nous avons besoin des coordonnées des points. En plus, chaque point peut comporter encore d’autres informations (attributs) tel que:
taille
couleur
étiquette
Dans un graphe social (Facebook), chaque nœud (utilisateur) possède un très grand nombre d’attributs, tels que: nom, prénom, âge, anniversaire, lieu de résidence, photo de profil, etc.
Exercice 5
Ajoutez un point supplémentaire pour Berne. Choisissez les coordonnées, la taille, couleur et l’étiquette. Ajoutez une connexion pour Berne-Fribourg, et Berne-Vevey.
15.9. Attribut des lignes¶
Chaque ligne peut avoir des attributs. Pour un graphe dessiné, ceci peut être la couleur et l’épaisseur du trait.
Dans le cas général, par exemple pour un réseau de transportation (Google Map), les attributs de lignes peuvent être:
distance (en km)
durée du parcours (en minutes)
cout en essence (en francs)
cout en péage (en francs)
Ces informations permettent à Google Map de trouver par exemple le chemin
le plus court
le plus rapide
le plus écologique
le meilleur marché
Exercice 6
Ajoutez des connexions supplémentaires pour Geneva-Fribourg et Fribourg-Vevey. Choisissez une couleur et une épaisseur appropriée.
15.10. Points aléatoires¶
Nous allons utiliser la fonction aléatoire randint() pour créer des coordonnées qui se trouvent à l’intérieur du canevas.
Nous commençons avec une liste vide points = [] et dans une boucle nous ajoutons les points.
La fonction seed(2) sert à avoir exactement la même configuration à chaque fois quand le programme est lancé.
Vous pouvez changer le paramètre pour seed() pour avoir une autre distribution aléatoire.
Graphe circulaire¶
Nous allons utiliser la fonction aléatoire randint() pour créer des coordonnées qui se trouvent à l’intérieur du canevas.
Nous commençons avec une liste vide points = [] et dans une boucle nous ajoutons les points.
La fonction seed(2) sert à avoir exactement la même configuration à chaque fois quand le programme est lancé.
Vous pouvez changer le paramètre pour seed() pour avoir une autre distribution aléatoire.
Exercice 7
Modifiez la couleur des points à 'lime' et leur diamètre à 10+4*i, pour que leur taille soit proportionnelle à leur indice.
Graphe étoilé¶
Nous commençons avec une liste vide lignes = [] et nous ajoutons
dans une boucle une ligne (0, i) qui va du point 0 vers tous les autres points.
Graphe roue¶
Nous commençons avec une liste vide lignes = [] et dans une boucle nous ajoutons :
une ligne
(0, i)qui va du point 0 vers tous les autres points,une ligne
(i-1, i)qui relie tous les points extérieurs.
Graphe arbre¶
Un graphe arbre évoque la ramification des branches d’un arbre. En théorie des graphes, un arbre est un graphe acyclique, donc sans des parcours circulaires. Dans un arbre chaque point est lié à chaque autre point par un seul chemin.
Graphe complet¶
Dans un graphe complet, tout point est lié à tous les autres points.
Nous utilisons une boucle imbriquée avec les deux variables d’itération i et j, pour calculer toutes les combinaisons.
15.11. Exercice¶
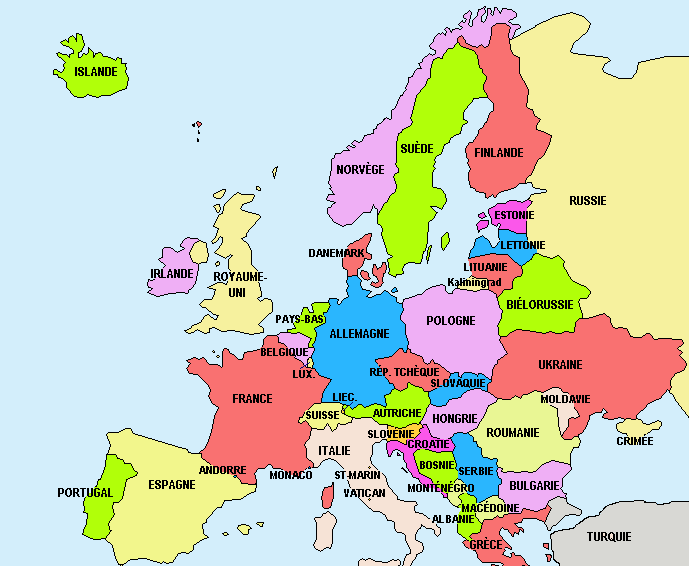
Pays voisins¶
Créez un graphe avec les pays d’Europe. Chaque pays est un nœud. Si les pays sont voisins, ils possèdent un lien entre eux.
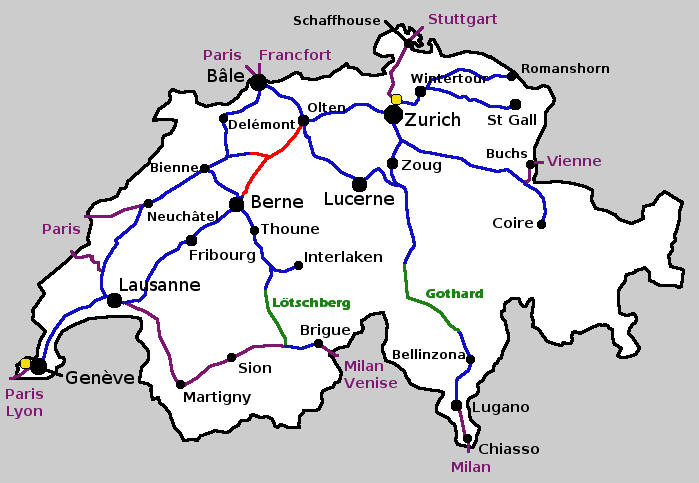
Réseau ferroviaire¶
Créez un graphe qui représente le réseau ferroviaire suisse. Chaque ville est un nœud. Les lignes de chemin de fer représentent les liens.