4. Les images¶
4.1. Les images matricielles¶
Depuis des siècles les humains gardent des traces de leur environnement sous forme d’images. Plus le temps passe, plus ces traces sont fidèles. On découvre par exemple la perspective autour du XVe siècle, les progrès en optique et en chimie permettent ensuite la création de la camera obscura et de la photographie argentique. Enfin l’informatique se développe permettant l’invention de la photographie numérique.
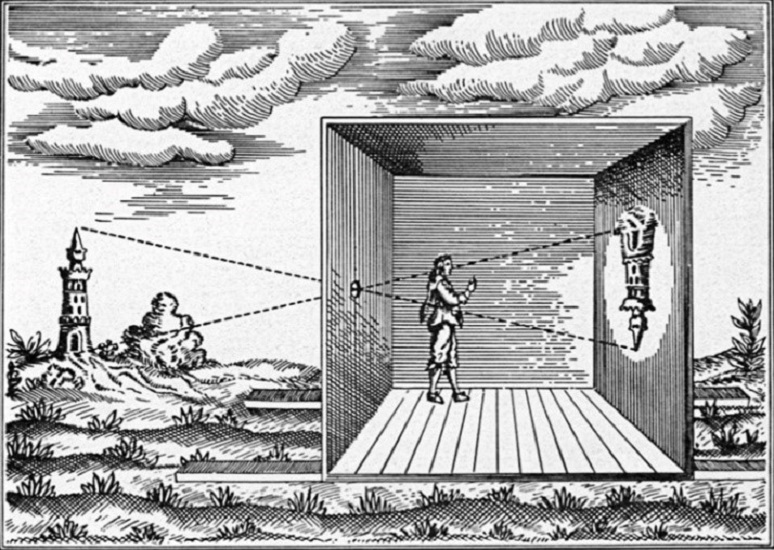
Fig. 4.1 Principe de fonctionnement de la camera obscura.¶

Fig. 4.2 Une caméra obscura.¶
De la camera obscura à la caméra numérique¶
Comment fonctionne une caméra numérique ? Une caméra numérique fonctionne en fait d’une manière très similaire à la caméra obscura et aux appareils photographiques analogiques d’un point de vue optique. Imaginez une chambre noire pourvue d’un trou sur l’une de ses parois. La lumière venant de l’extérieur vient se projeter sur le mur opposé.
Dans un appareil analogique, la paroi illuminée est recouverte d’une pellicule chimique photosensible qui permet de capturer l’image.
La différence est que dans un appareil photo numérique cette paroi, le capteur photographique, est recouverte d’une grille de capteurs électroniques photosensibles (photosites) produisant de l’électricité quand ils reçoivent de la lumière. Chaque photosite est recouvert d’un filtre coloré ne laissant passer que les rayons d’une seule couleur (grille de Bayer): le rouge, le vert ou le bleu. Les filtres sont répartis par carré de quatre : deux verts, un rouge et un bleu. La tension électrique produite par chaque photosite est convertie numériquement et transmise au processeur de l’appareil photo.
L’image numérique ne sera alors rien d’autre que la collection des mesures de tous les capteurs à un temps précis. Comme ces mesures sont organisées sous forme de tableau (grille), on parle souvent d’images matricielles. Plus le nombre de capteurs est grand, plus la définition de cette image le sera aussi.
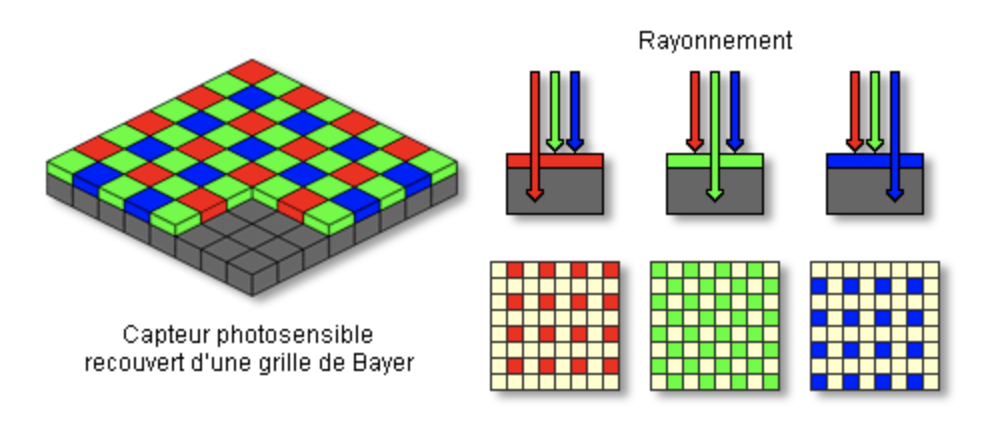
Fig. 4.3 Principe de la capture numérique d’une image.¶
4.2. Représentation d’une image en noir et blanc¶
Un bit est l’unité minimale d’information qu’un ordinateur manipule : 1 ou 0, allumé ou éteint. L’image la plus simple qu’un ordinateur puisse afficher est constituée uniquement de noir et blanc. Ainsi, un pixel pourrait être à l’état soit «noir», soit «blanc».

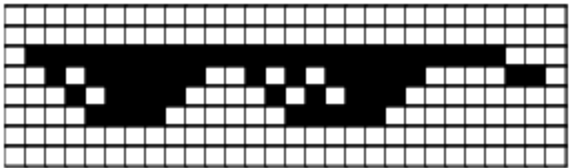
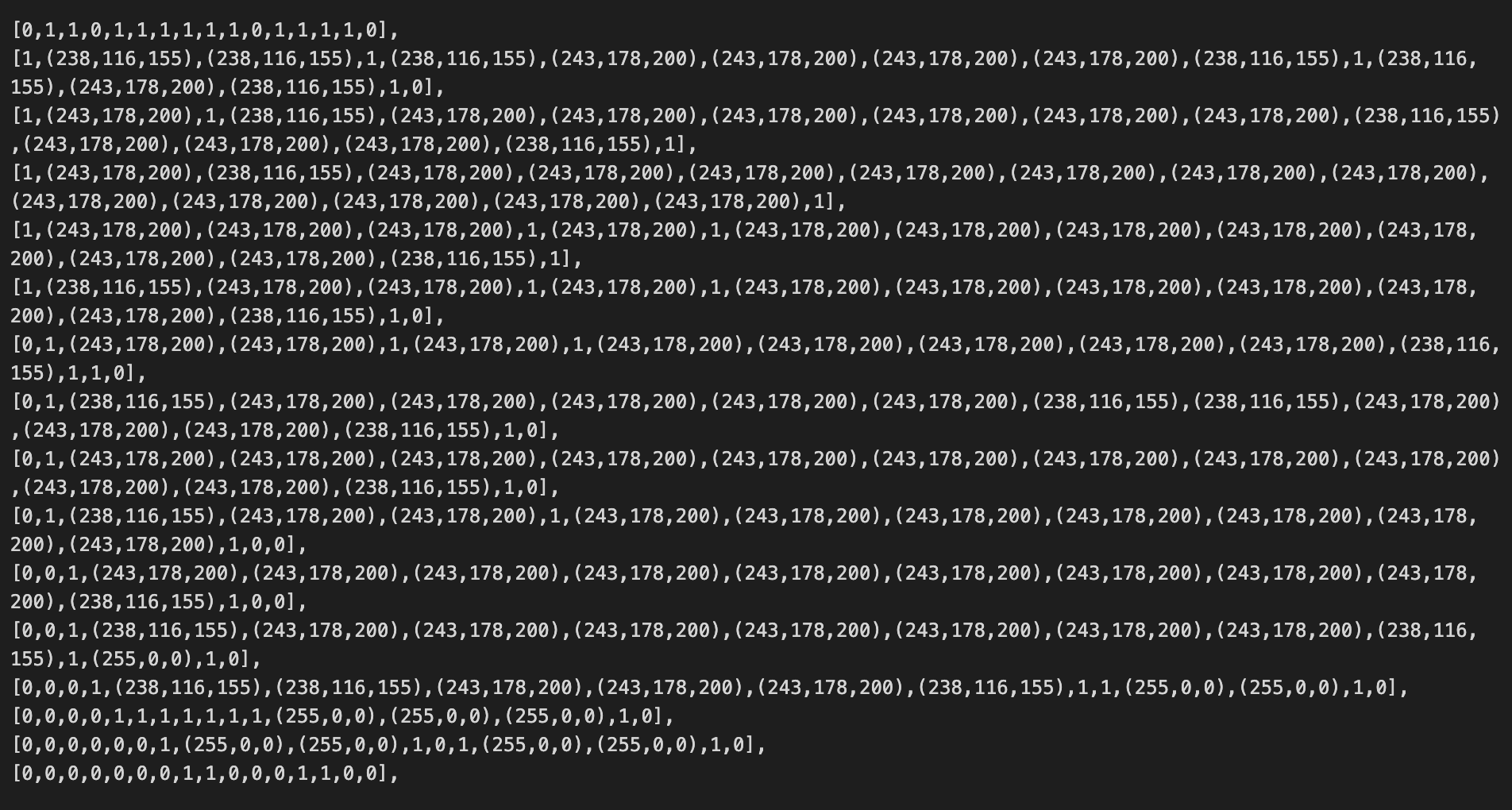
Fig. 4.4 Tous les pixels marqués d’un 1 s’affichent en blanc, tous ceux marqués d’un 0 s’affichent en noir. Ceci nous permet de construire des images simples, dessinées seulement en noir et blanc.¶
Un pixel, de l’anglais “picture element”, est le composant minimal d’une image. C’est à dire que c’est le plus petit élément avec lequel on construit une image sur un écran d’ordinateur. Dans notre exemple minimaliste, chaque pixel peut être soit noir, soit blanc, ce qui nous permet de construire une image.
4.3. Représentation d’une image en niveaux de gris¶
Dans ce type d’image seul le niveau de l’intensité est codé sur un octet (256 valeurs). Par convention, la valeur 0 représente le noir (intensité lumineuse nulle) et la valeur 255 le blanc (intensité lumineuse maximale) :

Fig. 4.5 Niveaux de gris, codage sur 8 bits.¶
En général, les images sont représentées sous forme de tableau numérique, aussi appelé format matriciel. Une image en niveau de gris sera ainsi représentée par un tableau de valeurs correspondant à la luminance de chaque pixel. Les valeurs de luminance sont des nombres allant de 0 (noir) à 255 (blanc). Pour encoder une image en niveaux de gris, chaque pixel nécessite donc 8 bits.

Fig. 4.6 Image monochrome, pixels et luminance.¶
Pour accéder à un pixel particulier, il faut indiquer à quelle ligne et à quelle colonne de l’image ce pixel se trouve. Le pixel (0,0) correspondra normalement au pixel de la première ligne et de la première colonne.
Le saviez-vous ?
Ce mode de fonctionnement est similaire à celui des tableurs pour lesquels il est possible d’accéder à la valeur d’une case en utilisant sa référence. On pourrait d’ailleurs utiliser le formatage conditionnel pour transformer un tableau de valeurs dans un tableur en image matricielle.
4.4. Représentation d’une image en couleurs¶
Le saviez-vous ?
The Million Dollar Homepage est un site web conçu en 2005 par Alex Tew, un étudiant anglais, dans le but de financer ses études supérieures. La page d’accueil est une grille de 1000 × 1000 pixels. Chaque pixel était vendu 1$ en tant qu’espace publicitaire. Ils ont tous été vendus…

En peinture, pour obtenir toutes les couleurs de l’arc-en-ciel, on utilise un mélange de magenta, de cyan et de jaune, qui vont chacune absorber une partie de la lumière ; c’est ce que l’on appelle la synthèse soustractive : en ajoutant du pigment à une surface, une partie du spectre lumineux est soustraite.
Pour faire la même chose sur un écran, on utilisera également trois couleurs, mais celles-ci seront le rouge, le vert et le bleu (couleurs primaires). Cela correspond à la synthèse additive : en allumant une LED rouge par exemple, on ajoute de la lumière sur la partie du spectre lumineux correspondant.

Fig. 4.7 Système additif et écran au microscope.¶
Chaque couleur est donc représentée comme un mélange de ces trois couleurs et donc sous forme de trois entiers (triplet). Comme pour les images en niveaux de gris, ces entiers sont généralement représentés sur 8 bits ; les valeurs de luminance sont chacune déclarées comme un nombre allant de 0 (intensité nulle) à 255 (intensité maximale). Pour représenter une image en couleurs il faut donc 8 bits pour le niveau de rouge, 8 bits pour le niveau de vert, et 8 bits pour le niveau de bleu, soit 24 bits.
Dans l’exemple qui suit, d’autres matrices de 0 et de 1 ont été configurées dans le programme, pour dessiner de nouveaux personnages. À la place de mario, essayez luigi, link, guerrier, tortueninja1, tortueninja2, homer, pikachu, kirby.
Conseil : à la place de mario, essayez luigi, link, guerrier, tortueninja1, tortueninja2, homer, pikachu, kirby, kirbycouleur.
Dans cette animation vous pouvez zoomer sur chacun des pixels qui constituent l’image totale. Chaque pixel possède trois valeurs allant de 0 à 255. RGB signifie en anglais Red, Green, Blue.
Dans cette autre animation vous pouvez jouer avec la valeur de Rouge, Vert, Bleu, pour créer une couleur finale. L’outil vous permet d’abord de jouer avec des couleurs codées en 24 bits, puis en 8 bits, ce qui illustre bien la précision qu’on arrive à atteindre avec 24 bits.
Les formats matriciels sont Portable Network Graphics (.png), Joint Photographic Experts Group (.jpeg), Tagged Image File Format (.tiff), BITMAP (.bmp), Graphics Interchange Format (.gif) pour citer les plus courants.
Définition et résolution¶
On appelle définition le nombre de points (pixel) constituant l’image, c’est-à-dire sa « dimension informatique » (le nombre de colonnes de l’image que multiplie son nombre de lignes). Une image possédant 640 pixels en largeur et 480 en hauteur aura une définition de 640 pixels par 480, notée 640x480 soit 307200 pixels.
La résolution, terme souvent confondu avec la définition, détermine en revanche le nombre de points par unité de longueur, exprimé en points par pouce (PPP, en anglais DPI pour Dots Per Inch), un pouce représentant 2.54 cm. La résolution permet ainsi d’établir le rapport entre le nombre de pixels d’une image et la taille réelle de sa représentation sur un support physique. Une résolution de 300 dpi signifie donc 300 colonnes et 300 rangées de pixels sur un pouce carré, ce qui donne donc 90000 pixels sur un pouce carré. La résolution de référence de 72 dpi nous donne un pixel de 1/72 (un pouce divisé par 72) soit 0.353 mm, correspondant à un point pica (unité typographique anglo saxonne).
Les dimensions d’une image sont donc définies par :
largeur = nombre de colonnes / résolution,
hauteur = nombre de lignes / résolution.
Compression¶
La plupart de ces formats utilisent des algorithmes de compression, afin de réduire la taille de l’image sur les mémoires de masse de l’ordinateur (disque durs, …).
On définit alors le taux de compression par : (1 - (taille du fichier image))/(taille de l’image en mémoire)
La compression peut être réalisée avec ou sans perte :
sans perte : l’image comprimée est parfaitement identique à l’originale,
avec perte : l’image est plus ou moins dégradée, selon le taux de compression souhaité.
4.5. Les images vectorielles¶
Pour reproduire une image sur une feuille, on peut la diviser en grille et définir un niveau de gris pour chaque case, mais on peut aussi tout simplement dessiner une figure, par exemple un trait d’un millimètre d’épaisseur allant d’un point A à un point B de l’image. De la même manière, en informatique, il est possible de représenter des images sous forme de grilles de pixels, comme nous l’avons vu, mais il est en effet également possible de définir une image comme une collection d’objets graphiques élémentaires (un segment, un carré, une ellipse…) sur un espace plan : c’est le principe des images vectorielles.
L’image vectorielle est dépourvue de matrice. Elle est en fait créée à partir d’équations mathématiques. Cette image numérique est composée d’objets géométriques individuels, des primitives géométriques (segments de droite, arcs de cercle, polygones, etc.), définies chacunes par différents attributs (forme, position, couleur, remplissage, visibilité, etc.) et auxquels on peut appliquer différentes transformations (rotations, écrasement, mise à l’échelle, inclinaison, effet miroir, symétrie, translation, et bien d’autres …).

Fig. 4.8 Un même cercle en représentation matricielle et vectorielle.¶
À l’inverse de l’image matricielle composée de pixels, l’image vectorielle peut être redimensionnée sans pour autant perdre en qualité. Elle est contenue dans un fichier beaucoup plus léger qu’une image pixelisée, indépendamment de sa taille et de sa définition. En revanche, chaque forme d’une image vectorielle est remplie d’une seule couleur dite solide ou d’un dégradé de couleurs. Elle reste donc limitée en termes de réalisme, et donc inutilisable en photographie par exemple. De plus une image vectorielle ne peut être créée qu’à partir d’un logiciel dédié, et n’est pas reconnue par les navigateurs internet.
Les formats vectoriels les plus courants sont Postscript (.ps) et Encapsulé Postscript (.eps), Adobe Illustrator (AI), Portable Document Format (PDF), WMF (format Windows).
Micro-activité
Saisissez le texte suivant dans un éditeur de texte et enregistrer le sous forme de fichier .svg. Il vous sera ensuite normalement possible d’ouvrir ce fichier avec un logiciel pour afficher les images.
<svg width="100" height="100" version="1.1" xmlns="http://www.w3.org/2000/svg">
<circle cx="50" cy="50" r="40" stroke="black" stroke-width="2" fill="red"/>
</svg>
Modifier le fichier afin de dessiner quatre carrés différents.
Pour aller plus loin
Identifiez et listez les avantages et les inconvénients du format vectoriel en comparaison avec le système matriciel.
4.6. Bonus¶
Une œuvre d’art numérique signée Andreas Gysin …
4.7. Exercices¶
Exercice 1 – Définition
Quelle est la définition d’une feuille scannée de largeur 6,5 pouces, de hauteur 9 pouces en 400 dpi ?
Exercice 2 – Carte graphique
1 - Calculer, pour chaque définition d’image et chaque couleur, la taille mémoire nécessaire à l’affichage.
Définition de l’image |
Noir et blanc |
256 couleurs |
65000 couleurs |
True color |
|---|---|---|---|---|
320x200 |
||||
640x480 |
||||
800x600 |
||||
1024x768 |
Réponse
2 - Que signifie la valeur 2.3 Mo dans le tableau résultat ?
Réponse
Exercice 3 – Compression
Une image de couleur a pour format : 360 × 270. Elle est enregistrée en bitmap 8 bits. Quelle est sa taille sur le disque dur (détaillez les calculs) ?
Une image noir et blanc de format 1024 × 1024 est enregistrée en JPG. Le taux de compression est de 50%. Quelle est sa taille sur le disque dur (détaillez les calculs) ?
Réponse
Exercice 4 – Appareil photo
L’appareil numérique FinePix2400Z (Fujifilm) permet la prise de vue avec trois définitions : a) 640x480 pixels ; b) 1280x960 pixels ; c) 1600x1200 pixels.
Calculez la taille de l’image non-compressée pour chaque définition.
Exercice 5 – Pixelisation
Une image numérique de définition 1024×768 mesure 30 cm de large et 20 cm de haut.
Déterminez les dimensions des pixels.
On a une photographie de 10 cm sur 5 cm que l’on scanne avec une résolution de 300 ppi. Quelle sera alors la taille de l’image (en nombre de pixels) ?
Soit une image 15×9 cm, définie en RVB, que l’on scanne en 72, 300 et 1200 ppi. Quels seront les poids des images, pour une profondeur de 16 bits par couleur ?